Liczby zespolone są minimalnym rozszerzeniem znanego nam zbioru liczb rzeczywistych. Ich zasadnicza różnica polega na tym, że pojawia się element, który po podniesieniu do kwadratu daje -1, tj. ja lub .

Każda liczba zespolona składa się z dwóch części: prawdziwe i wyimaginowane:

Zatem jasne jest, że zbiór liczb rzeczywistych pokrywa się ze zbiorem liczb zespolonych z zerową częścią urojoną.

Najpopularniejszym modelem zbioru liczb zespolonych jest zwykła płaszczyzna. Pierwsza współrzędna każdego punktu będzie jego częścią rzeczywistą, a druga częścią urojoną. Wtedy rolą samych liczb zespolonych będą wektory mające początek w punkcie (0,0).

Operacje włączone Liczby zespolone.

Tak naprawdę, jeśli weźmiemy pod uwagę model zbioru liczb zespolonych, intuicyjnie widać, że dodawanie (odejmowanie) i mnożenie dwóch liczb zespolonych wykonuje się w taki sam sposób, jak odpowiadające im operacje na wektorach. Co więcej, mamy na myśli iloczyn wektorowy wektorów, ponieważ wynikiem tej operacji jest ponownie wektor.

1.1 Dodatek.

(Jak widać, ta operacja odpowiada dokładnie)

1.2 Odejmowanie podobnie wytwarza się według następującej zasady:

2. Mnożenie.

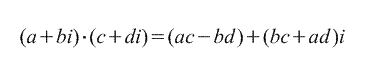
3. Podział.

Zdefiniowane po prostu jako odwrotna operacja mnożenia.

Forma trygonometryczna.

Moduł liczby zespolonej z jest następującą wielkością:

,

oczywiście jest to znowu tylko moduł (długość) wektora (a, b).

Najczęściej moduł liczby zespolonej oznacza się jako ρ.

Okazało się, że

z = ρ(cosφ+isinφ).

Poniższe wynika bezpośrednio z trygonometrycznej formy zapisu liczby zespolonej: formuły :

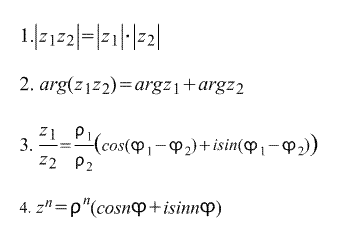
Ostatnia formuła nazywa się Wzór Moivre’a. Formuła wywodzi się bezpośrednio z niego n-ty pierwiastek liczby zespolonej:

zatem istnieje n n-tych pierwiastków liczby zespolonej z.

Plan lekcji.

1. Moment organizacyjny.

2. Prezentacja materiału.

3. Praca domowa.

4. Podsumowanie lekcji.

Podczas zajęć

I. Moment organizacyjny.

II. Prezentacja materiału.

Motywacja.

Rozbudowa zbioru liczb rzeczywistych polega na dodaniu nowych liczb (urojonych) do liczb rzeczywistych. Wprowadzenie tych liczb wynika z braku możliwości wyodrębnienia pierwiastka z liczby ujemnej w zbiorze liczb rzeczywistych.

Wprowadzenie do pojęcia liczby zespolonej.

Liczby urojone, którymi uzupełniamy liczby rzeczywiste, zapisuje się w postaci bi, Gdzie I jest jednostką urojoną, oraz ja 2 = - 1.

Na tej podstawie otrzymujemy następująca definicja Liczba zespolona.

Definicja. Liczba zespolona jest wyrazem postaci a+bi, Gdzie A I B- liczby rzeczywiste. W tym przypadku spełnione są następujące warunki:

a) Dwie liczby zespolone za 1 + b 1 ja I za 2 + b 2 ja równe wtedy i tylko wtedy, gdy za 1 = za 2, b 1 = b 2.

b) Dodawanie liczb zespolonych określa zasada:

(za 1 + b 1 ja) + (za 2 + b 2 ja) = (za 1 + za 2) + (b 1 + b 2) ja.

c) Mnożenie liczb zespolonych określa zasada:

(za 1 + b 1 ja) (za 2 + b 2 ja) = (za 1 za 2 - b 1 b 2) + (za 1 b 2 - za 2 b 1) ja.

Postać algebraiczna liczby zespolonej.

Zapisywanie liczby zespolonej w postaci a+bi nazywa się formą algebraiczną liczby zespolonej, gdzie A– część prawdziwa, bi jest częścią urojoną, oraz B- prawdziwy numer.

Liczba zespolona a+bi uważa się za równy zeru, jeśli jego część rzeczywista i urojona są równe zeru: a = b = 0

Liczba zespolona a+bi Na b = 0 uważa się za liczbę rzeczywistą A: a + 0i = a.

Liczba zespolona a+bi Na a = 0 nazywa się czysto urojonym i jest oznaczane bi: 0 + bi = bi.

Dwie liczby zespolone z = a + bi I = a – bi, różniące się jedynie znakiem części urojonej, nazywane są sprzężonymi.

Działania na liczbach zespolonych w postaci algebraicznej.

Na liczbach zespolonych w formie algebraicznej można wykonać następujące operacje.

1) Dodatek.

Definicja. Suma liczb zespolonych z 1 = za 1 + b 1 ja I z 2 = za 2 + b 2 ja nazywa się liczbą zespoloną z, którego część rzeczywista jest równa sumie części rzeczywistych z 1 I z 2, a część urojona jest sumą części urojonych liczb z 1 I z 2, to jest z = (za 1 + za 2) + (b 1 + b 2)i.

Liczby z 1 I z 2 nazywane są terminami.

Dodawanie liczb zespolonych ma następujące właściwości:

1°. Przemienność: z 1 + z 2 = z 2 + z 1.

2°. Łączność: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).

3°. Liczba zespolona –a –bi nazywana przeciwieństwem liczby zespolonej z = a + bi. Liczba zespolona, ​​przeciwieństwo liczby zespolonej z, oznaczony -z. Suma liczb zespolonych z I -z równe zeru: z + (-z) = 0

Przykład 1: Wykonaj dodawanie (3 – i) + (-1 + 2i).

(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) ja = 2 + 1i.

2) Odejmowanie.

Definicja. Odejmij od liczby zespolonej z 1 Liczba zespolona z 2 z, Co z + z 2 = z 1.

Twierdzenie. Różnica między liczbami zespolonymi istnieje i jest wyjątkowa.

Przykład 2: Wykonaj odejmowanie (4 – 2i) - (-3 + 2i).

(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.

3) Mnożenie.

Definicja. Iloczyn liczb zespolonych z 1 = a 1 + b 1 ja I z 2 = a 2 + b 2 ja nazywa się liczbą zespoloną z, określone przez równość: z = (za 1 za 2 – b 1 b 2) + (za 1 b 2 + za 2 b 1)i.

Liczby z 1 I z 2 nazywane są czynnikami.

Mnożenie liczb zespolonych ma następujące właściwości:

1°. Przemienność: z 1 z 2 = z 2 z 1.

2°. Łączność: (z 1 z 2) z 3 = z 1 (z 2 z 3)

3°. Rozdzielność mnożenia względem dodawania:

(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3.

4°. z = (a + bi)(a – bi) = za 2 + b 2- prawdziwy numer.

W praktyce mnożenie liczb zespolonych odbywa się według zasady mnożenia sumy przez sumę i oddzielania części rzeczywistej od urojonej.

W poniższym przykładzie rozważymy mnożenie liczb zespolonych na dwa sposoby: według reguły i mnożąc sumę przez sumę.

Przykład 3: Wykonaj mnożenie (2 + 3i) (5 – 7i).

1 sposób. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + ja.

Metoda 2. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.

4) Podział.

Definicja. Dzielenie liczby zespolonej z 1 do liczby zespolonej z 2, oznacza znalezienie takiej liczby zespolonej z, Co z · z 2 = z 1.

Twierdzenie. Iloraz liczb zespolonych istnieje i jest unikalny, jeśli z 2 ≠ 0 + 0i.

W praktyce iloraz liczb zespolonych oblicza się, mnożąc licznik i mianownik przez sprzężenie mianownika.

Pozwalać z 1 = za 1 + b 1 ja, z 2 = za 2 + b 2 ja, Następnie

.

W poniższym przykładzie wykonamy dzielenie, korzystając ze wzoru i zasady mnożenia przez liczbę sprzężoną z mianownikiem.

Przykład 4. Znajdź iloraz .

5) Podniesienie do dodatniej potęgi całkowitej.

a) Potęgi jednostki urojonej.

Korzystanie z równości ja 2 = -1, łatwo jest zdefiniować dowolną dodatnią moc całkowitą jednostki urojonej. Mamy:

ja 3 = ja 2 ja = -i,

ja 4 = ja 2 ja 2 = 1,

ja 5 = ja 4 ja = ja,

ja 6 = ja 4 i 2 = -1,

ja 7 = ja 5 i 2 = -i,

ja 8 = ja 6 i 2 = 1 itp.

To pokazuje, że wartości stopni W, Gdzie N– dodatnia liczba całkowita, powtarzana okresowo w miarę wzrostu wskaźnika o 4 .

Dlatego należy zwiększyć liczbę I do dodatniej potęgi całkowitej, musimy podzielić wykładnik przez 4 i budować I do potęgi, której wykładnik jest równy reszcie dzielenia.

Przykład 5: Oblicz: (i 36 + i 17) i 23.

ja 36 = (i 4) 9 = 1 9 = 1,

ja 17 = ja 4 × 4+1 = (i 4) 4 × ja = 1 · ja = ja.

ja 23 = ja 4 × 5+3 = (i 4) 5 × ja 3 = 1 · ja 3 = - ja.

(i 36 + ja 17) · ja 23 = (1 + i) (- i) = - ja + 1= 1 – ja.

b) Podnoszenie liczby zespolonej do dodatniej potęgi całkowitej odbywa się zgodnie z zasadą podnoszenia dwumianu do odpowiedniej potęgi, ponieważ jest to szczególny przypadek mnożenia identycznych czynników zespolonych.

Przykład 6: Oblicz: (4 + 2i) 3

(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.