Calculate z and plot on the complex plane. Modulus and argument of a complex number. Trigonometric. Introduction to the concept of a complex number
Complex numbers are the minimal extension of the set of real numbers we are familiar with. Their fundamental difference is that an element appears that gives -1 when squared, i.e. i, or .
Any complex number consists of two parts: real and imaginary:
Thus, it is clear that the set of real numbers coincides with the set of complex numbers with a zero imaginary part.
The most popular model for the set of complex numbers is the ordinary plane. The first coordinate of each point will be its real part, and the second will be its imaginary part. Then the role of the complex numbers themselves will be vectors with the beginning at the point (0,0).
Operations on complex numbers.
In fact, if we take into account the model of the set of complex numbers, it is intuitively clear that addition (subtraction) and multiplication of two complex numbers are performed in the same way as the corresponding operations on vectors. Moreover, we mean the vector product of vectors, because the result of this operation is again a vector.
1.1 Addition.
(As you can see, this operation corresponds exactly to)
1.2 Subtraction, similarly, is produced according to the following rule:
2. Multiplication.
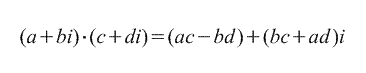
3. Division.
Defined simply as the inverse operation of multiplication.

Trigonometric form.
The modulus of a complex number z is the following quantity:
 ,
,
obviously, this is, again, just the modulus (length) of the vector (a,b).
Most often, the modulus of a complex number is denoted as ρ.
It turns out that
z = ρ(cosφ+isinφ).
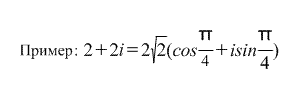
The following follows directly from the trigonometric form of writing a complex number: formulas :
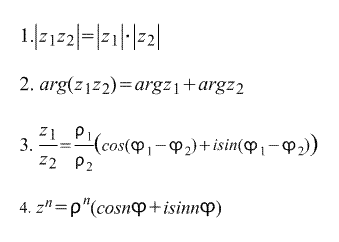
The last formula is called Moivre's formula. The formula is derived directly from it nth root of a complex number:

thus, there are n nth roots of the complex number z.
Lesson plan.
1. Organizational moment.
2. Presentation of the material.
3. Homework.
4. Summing up the lesson.
During the classes
I. Organizational moment.
II. Presentation of the material.
Motivation.
The expansion of the set of real numbers consists of adding new numbers (imaginary) to the real numbers. The introduction of these numbers is due to the impossibility of extracting the root of a negative number in the set of real numbers.
Introduction to the concept of a complex number.
Imaginary numbers, with which we complement real numbers, are written in the form bi, Where i is an imaginary unit, and i 2 = - 1.
Based on this, we get following definition complex number.
Definition. A complex number is an expression of the form a+bi, Where a And b- real numbers. In this case, the following conditions are met:
a) Two complex numbers a 1 + b 1 i And a 2 + b 2 i equal if and only if a 1 =a 2, b 1 =b 2.
b) The addition of complex numbers is determined by the rule:
(a 1 + b 1 i) + (a 2 + b 2 i) = (a 1 + a 2) + (b 1 + b 2) i.
c) Multiplication of complex numbers is determined by the rule:
(a 1 + b 1 i) (a 2 + b 2 i) = (a 1 a 2 - b 1 b 2) + (a 1 b 2 - a 2 b 1) i.
Algebraic form of a complex number.
Writing a complex number in the form a+bi is called the algebraic form of a complex number, where A– real part, bi is the imaginary part, and b– real number.
Complex number a+bi is considered equal to zero if its real and imaginary parts are equal to zero: a = b = 0
Complex number a+bi at b = 0 considered to be the same as a real number a: a + 0i = a.
Complex number a+bi at a = 0 is called purely imaginary and is denoted bi: 0 + bi = bi.
Two complex numbers z = a + bi And = a – bi, differing only in the sign of the imaginary part, are called conjugate.
Operations on complex numbers in algebraic form.
You can perform the following operations on complex numbers in algebraic form.
1) Addition.
Definition. Sum of complex numbers z 1 = a 1 + b 1 i And z 2 = a 2 + b 2 i is called a complex number z, the real part of which is equal to the sum of the real parts z 1 And z 2, and the imaginary part is the sum of the imaginary parts of numbers z 1 And z 2, that is z = (a 1 + a 2) + (b 1 + b 2)i.
Numbers z 1 And z 2 are called terms.
Addition of complex numbers has the following properties:
1º. Commutativity: z 1 + z 2 = z 2 + z 1.
2º. Associativity: (z 1 + z 2) + z 3 = z 1 + (z 2 + z 3).
3º. Complex number –a –bi called the opposite of a complex number z = a + bi. Complex number, opposite of complex number z, denoted -z. Sum of complex numbers z And -z equal to zero: z + (-z) = 0
Example 1: Perform addition (3 – i) + (-1 + 2i).
(3 – i) + (-1 + 2i) = (3 + (-1)) + (-1 + 2) i = 2 + 1i.
2) Subtraction.
Definition. Subtract from a complex number z 1 complex number z 2 z, What z + z 2 = z 1.
Theorem. The difference between complex numbers exists and is unique.
Example 2: Perform a subtraction (4 – 2i) - (-3 + 2i).
(4 – 2i) - (-3 + 2i) = (4 - (-3)) + (-2 - 2) i = 7 – 4i.
3) Multiplication.
Definition. Product of complex numbers z 1 =a 1 +b 1 i And z 2 =a 2 +b 2 i is called a complex number z, defined by the equality: z = (a 1 a 2 – b 1 b 2) + (a 1 b 2 + a 2 b 1)i.
Numbers z 1 And z 2 are called factors.
Multiplication of complex numbers has the following properties:
1º. Commutativity: z 1 z 2 = z 2 z 1.
2º. Associativity: (z 1 z 2)z 3 = z 1 (z 2 z 3)
3º. Distributivity of multiplication relative to addition:
(z 1 + z 2) z 3 = z 1 z 3 + z 2 z 3.
4º. z = (a + bi)(a – bi) = a 2 + b 2- real number.
In practice, multiplication of complex numbers is carried out according to the rule of multiplying a sum by a sum and separating the real and imaginary parts.
In the following example, we will consider multiplying complex numbers in two ways: by rule and by multiplying sum by sum.
Example 3: Do the multiplication (2 + 3i) (5 – 7i).
1 way. (2 + 3i) (5 – 7i) = (2× 5 – 3× (- 7)) + (2× (- 7) + 3× 5)i = = (10 + 21) + (- 14 + 15 )i = 31 + i.
Method 2. (2 + 3i) (5 – 7i) = 2× 5 + 2× (- 7i) + 3i× 5 + 3i× (- 7i) = = 10 – 14i + 15i + 21 = 31 + i.
4) Division.
Definition. Divide a complex number z 1 to a complex number z 2, means to find such a complex number z, What z · z 2 = z 1.
Theorem. The quotient of complex numbers exists and is unique if z 2 ≠ 0 + 0i.
In practice, the quotient of complex numbers is found by multiplying the numerator and denominator by the conjugate of the denominator.
Let z 1 = a 1 + b 1 i, z 2 = a 2 + b 2 i, Then



 .
.
In the following example, we will perform division using the formula and the rule of multiplication by the number conjugate to the denominator.
Example 4. Find the quotient  .
.
5) Raising to a positive whole power.
a) Powers of the imaginary unit.
Taking advantage of equality i 2 = -1, it is easy to define any positive integer power of the imaginary unit. We have:
i 3 = i 2 i = -i,
i 4 = i 2 i 2 = 1,
i 5 = i 4 i = i,
i 6 = i 4 i 2 = -1,
i 7 = i 5 i 2 = -i,
i 8 = i 6 i 2 = 1 etc.
This shows that the degree values i n, Where n– a positive integer, periodically repeated as the indicator increases by 4 .
Therefore, to raise the number i to a positive whole power, we must divide the exponent by 4 and build i to a power whose exponent is equal to the remainder of the division.
Example 5: Calculate: (i 36 + i 17) i 23.
i 36 = (i 4) 9 = 1 9 = 1,
i 17 = i 4 × 4+1 = (i 4) 4 × i = 1 · i = i.
i 23 = i 4 × 5+3 = (i 4) 5 × i 3 = 1 · i 3 = - i.
(i 36 + i 17) · i 23 = (1 + i) (- i) = - i + 1= 1 – i.
b) Raising a complex number to a positive integer power is carried out according to the rule for raising a binomial to the corresponding power, since it is a special case of multiplying identical complex factors.
Example 6: Calculate: (4 + 2i) 3
(4 + 2i) 3 = 4 3 + 3× 4 2 × 2i + 3× 4× (2i) 2 + (2i) 3 = 64 + 96i – 48 – 8i = 16 + 88i.
Complex numbers
Imaginary And complex numbers. Abscissa and ordinate
complex number. Conjugate complex numbers.
Operations with complex numbers. Geometric
representation of complex numbers. Complex plane.
Modulus and argument of a complex number. Trigonometric
complex number form. Operations with complex
numbers in trigonometric form. Moivre's formula.
Basic information about imaginary And complex numbers are given in the section “Imaginary and complex numbers”. The need for these numbers of a new type arose when solving quadratic equations for the case
D< 0 (здесь D– discriminant of a quadratic equation). For a long time, these numbers did not find physical application, which is why they were called “imaginary” numbers. However, now they are very widely used in various fields of physics.and technology: electrical engineering, hydro- and aerodynamics, elasticity theory, etc.
Complex numbers are written in the form:a+bi. Here a And b – real numbers , A i – imaginary unit, i.e. e. i 2 = –1. Number a called abscissa,a b – ordinatecomplex numbera + bi.Two complex numbersa+bi And a–bi are called conjugate complex numbers.
Main agreements:
1. Real number
Acan also be written in the formcomplex number:a+ 0 i or a – 0 i. For example, records 5 + 0i and 5 – 0 imean the same number 5 .2. Complex number 0 + bicalled purely imaginary number. Recordbimeans the same as 0 + bi.
3. Two complex numbersa+bi Andc + diare considered equal ifa = c And b = d. Otherwise complex numbers are not equal.
Addition. Sum of complex numbersa+bi And c + diis called a complex number (a+c ) + (b+d ) i.Thus, when adding complex numbers, their abscissas and ordinates are added separately.
This definition corresponds to the rules for operations with ordinary polynomials.
Subtraction. The difference of two complex numbersa+bi(diminished) and c + di(subtrahend) is called a complex number (a–c ) + (b–d ) i.
Thus, When subtracting two complex numbers, their abscissas and ordinates are subtracted separately.
Multiplication. Product of complex numbersa+bi And c + di is called a complex number:
(ac–bd ) + (ad+bc ) i.This definition follows from two requirements:
1) numbers a+bi And c + dimust be multiplied like algebraic binomials,
2) number ihas the main property:i 2 = – 1.
EXAMPLE ( a+ bi )(a–bi) = a 2 +b 2 . Hence, work
two conjugate complex numbers is equal to the real
a positive number.
Division. Divide a complex numbera+bi (divisible) by anotherc + di(divider) - means to find the third numbere + f i(chat), which when multiplied by a divisorc + di, results in the dividenda + bi.
If the divisor is not zero, division is always possible.
EXAMPLE Find (8 +i ) : (2 – 3 i) .
Solution. Let's rewrite this ratio as a fraction:
Multiplying its numerator and denominator by 2 + 3i
AND Having performed all the transformations, we get:

Geometric representation of complex numbers. Real numbers are represented by points on the number line:
Here is the point Ameans the number –3, dotB– number 2, and O- zero. In contrast, complex numbers are represented by points on the coordinate plane. For this purpose, we choose rectangular (Cartesian) coordinates with the same scales on both axes. Then the complex numbera+bi will be represented by a dot P with abscissa a and ordinate b (see picture). This coordinate system is called complex plane .
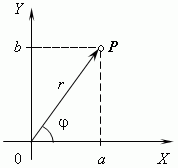
Module complex number is the length of the vectorOP, representing a complex number on the coordinate ( comprehensive) plane. Modulus of a complex numbera+bi denoted | a+bi| or letter r



